Leetcode solution 133: Clone Graph

Problem Statement 

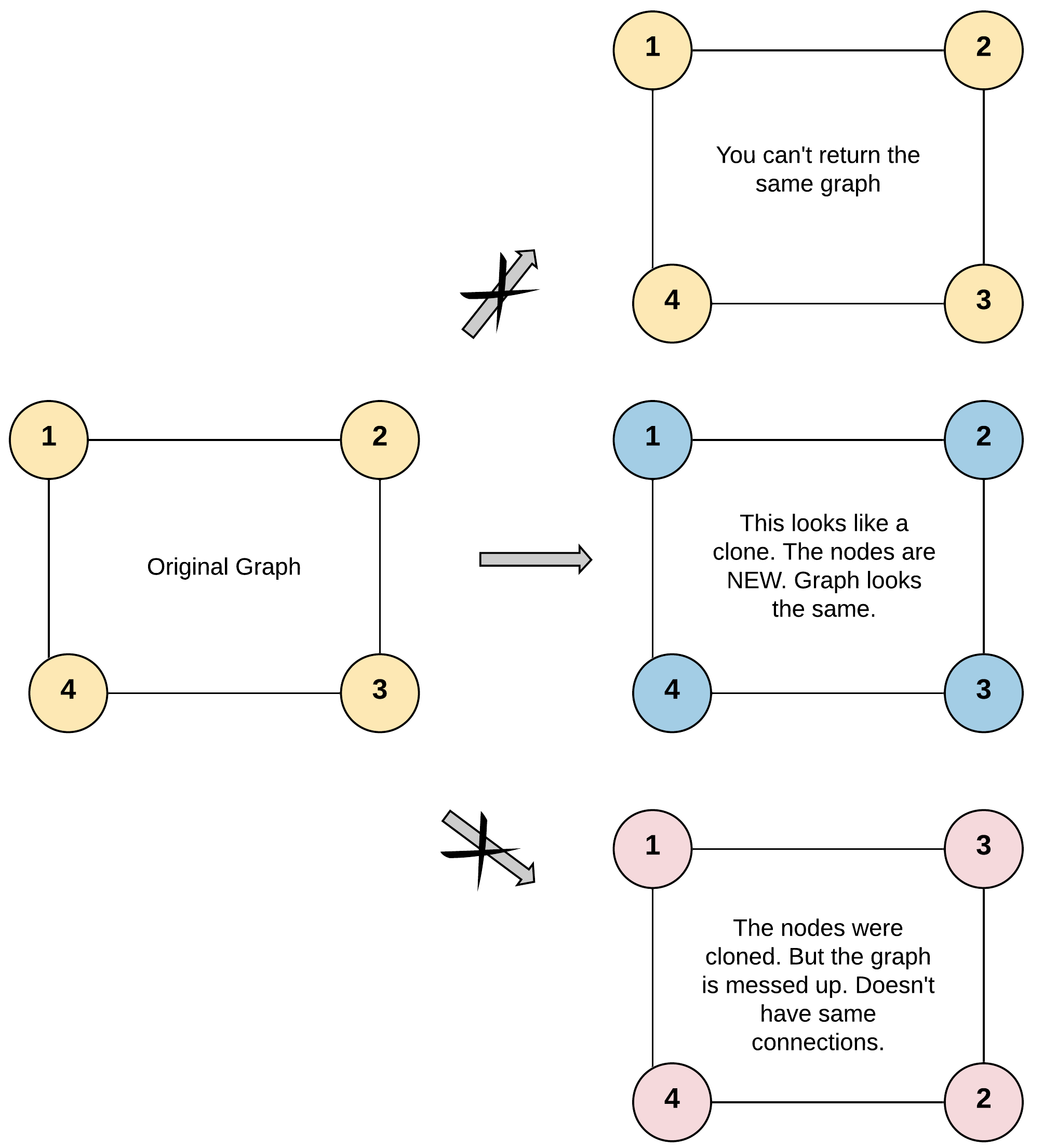
Given a reference of a node in a connected undirected graph.

Return a deep copy (clone) of the graph.

Each node in the graph contains a val (int) and a list (List[Node]) of its neighbors.

class Node {
    public int val;
    public List<Node> neighbors;
}

 

Test case format:

For simplicity sake, each node's value is the same as the node's index (1-indexed). For example, the first node with val = 1, the second node with val = 2, and so on. The graph is represented in the test case using an adjacency list.

Adjacency list is a collection of unordered lists used to represent a finite graph. Each list describes the set of neighbors of a node in the graph.

The given node will always be the first node with val = 1. You must return the copy of the given node as a reference to the cloned graph.

 

Example 1:

Input: adjList = [[2,4],[1,3],[2,4],[1,3]]
Output: [[2,4],[1,3],[2,4],[1,3]]
Explanation: There are 4 nodes in the graph.
1st node (val = 1)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
2nd node (val = 2)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
3rd node (val = 3)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
4th node (val = 4)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).

Example 2:

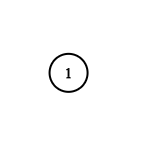
Input: adjList = [[]]
Output: [[]]
Explanation: Note that the input contains one empty list. The graph consists of only one node with val = 1 and it does not have any neighbors.

Example 3:

Input: adjList = []
Output: []
Explanation: This an empty graph, it does not have any nodes.

Example 4:

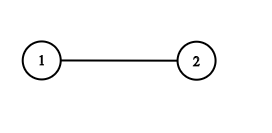
Input: adjList = [[2],[1]]
Output: [[2],[1]]

 

Constraints:

• 1 <= Node.val <= 100
• Node.val is unique for each node.
• Number of Nodes will not exceed 100.
• There is no repeated edges and no self-loops in the graph.
• The Graph is connected and all nodes can be visited starting from the given node.

Problem link

 

Video Tutorial

You can find the detailed video tutorial here

• Youtube
• B站

Thought Process

It's a basic graph problem that can be solved in 3 different ways: BFS using queue, DFS using recursion, DFS using stack(very similar to BFT using queue). The trick is using a map to keep a one-to-one mapping between the old nodes and the copied nodes, meanwhile, we can also use the map to avoid a cycle when performing BFS or DFS.

Solutions

BFS using queue

Time Complexity: O(N)
Space Complexity: O(N) the extra queue and map

DFS using recursion

Time Complexity: O(N)
Space Complexity: O(N) the extra map

DFS using stack

Time Complexity: O(N)
Space Complexity: O(N) the extra queue and stack

The main test method

References

• Leetcode official solution (download pdf)
• Code Ganker CSDN

Leetcode solution 135: Candy

Problem Statement 

There are N children standing in a line. Each child is assigned a rating value.

You are giving candies to these children subjected to the following requirements:

• Each child must have at least one candy.
• Children with a higher rating get more candies than their neighbors.

What is the minimum candies you must give?

Example 1:

Input: [1,0,2]
Output: 5
Explanation: You can allocate to the first, second and third child with 2, 1, 2 candies respectively.

Example 2:

Input: [1,2,2]
Output: 4
Explanation: You can allocate to the first, second and third child with 1, 2, 1 candies respectively.
             The third child gets 1 candy because it satisfies the above two conditions.

Problem link

 

Video Tutorial

You can find the detailed video tutorial here

• Youtube
• B站

Thought Process

The straight forward idea is go through the ranking array, for each ranking, we try to make sure it has more points than its left and right neighbor. Note that it’s not going to work if you just do that because while you are increasing the values, it’s a chain effect that will affect the previous values as well, therefore we have to go all the way to the beginning.

Use below ranking as an example, assume everyone has 1 point already
Ranking: [5, 3, 1]

Points [1, 0, 0]
When at 5, [1, 0, 0]
When at 3, [2, 1, 0]
When at 1, [2, 2, 1]
you might think 5 points is enough, but it’s wrong. The culprit is when you at 1, and increase child at 3, you have the potential to break the assumption that child with 3 ranking always has less than its left neighbor if that neighbor has more points. Therefore, we have to go all the way to the beginning and comparison, thus resulting O(N^2) time complexity

That said, we have to go all the way to the beginning when we increase any value, so in the end it looks like [3, 2, 1]

Hint: if you cannot solve it in one pass, can we solve it in two passes?

A more clever thought is trying to distribute the candies in two passes. Previously we are trying to ensure at certain point both the left and right constrains should met. With two passes, namely first pass (from left to right) ensure all the left neighbors constrains are satisfied, and second pass ensures all the right neighbors contains are satisfied.

• Left to right pass: Ensure I have more points than my left neighbor if my ranking is higher. Else I just have 1 candy (this is minimum)
• Right to left pass: Ensure I have more points than my right neighbor if my ranking is higher.

Solutions

Naive solution 

Time Complexity: O(N^2)
Space Complexity: O(N) the extra candies array

Two pass linear solution

Time Complexity: O(N)
Space Complexity: O(N) the extra candies array

References

• Leetcode discussion solution