直接上视频，建议1.5倍速收听😄
- 油管: https://youtu.be/D2JPb76-l78
- B站: https://www.bilibili.com/video/BV1Hv411v7UU/
【有没有觉得乔杉和习大大有那么一丢丢撞脸呀🤣】
Sunday, August 2, 2020
包子聊天系列：中年大叔程序员疫情之后往哪里跳？
Saturday, July 25, 2020
Leetcode solution 1344. Angle Between Hands of a Clock
Problem Statement
Given two numbers, hour and minutes. Return the smaller angle (in degrees) formed between the hour and the minute hand.
Example 1:
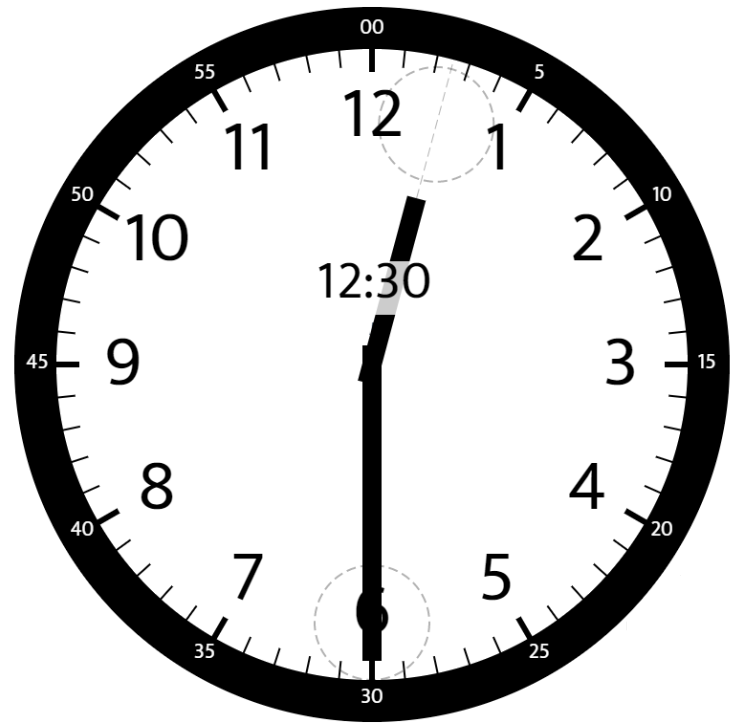
Input: hour = 12, minutes = 30 Output: 165
Example 2:
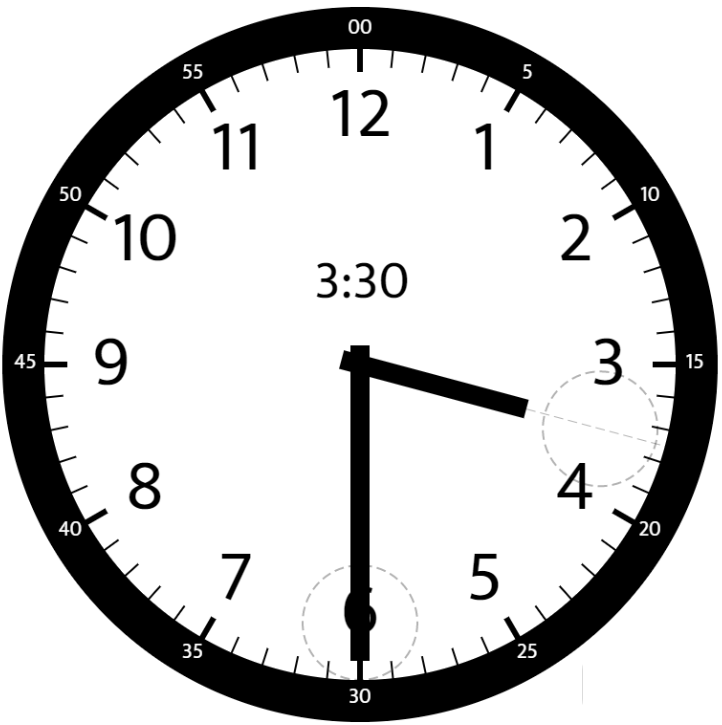
Input: hour = 3, minutes = 30 Output: 75
Example 3:
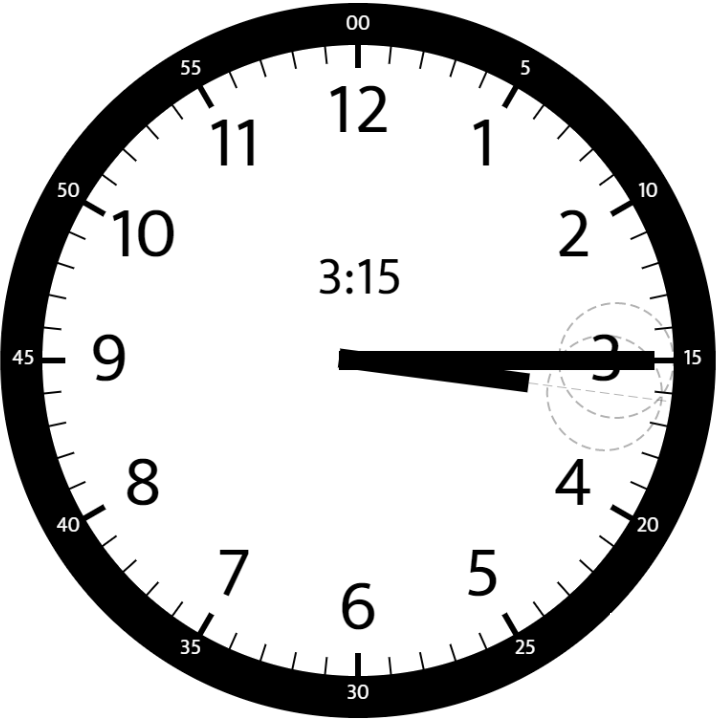
Input: hour = 3, minutes = 15 Output: 7.5
Example 4:
Input: hour = 4, minutes = 50 Output: 155
Example 5:
Input: hour = 12, minutes = 0 Output: 0
Constraints:
1 <= hour <= 120 <= minutes <= 59- Answers within
10^-5of the actual value will be accepted as correct.
Video Tutorial
You can find the detailed video tutorial hereThought Process
Purely a math problem. Calculate the clock's hour hand and minute hand separately.
- There are 60 minutes in 360 angle, so each minute is 6 degree in angle.
- Angle should be the absolute value of (minute angel - hour angle)
- Final angle should be min(angle, 360 - angle)
Solutions
Space Complexity: O(1) no extra space is used
References
Friday, July 17, 2020
Leetcode solution 1512. Number of Good Pairs
Problem Statement
Given an array of integers nums.
A pair (i,j) is called good if nums[i] == nums[j] and i < j.
Return the number of good pairs.
Example 1:
Input: nums = [1,2,3,1,1,3] Output: 4 Explanation: There are 4 good pairs (0,3), (0,4), (3,4), (2,5) 0-indexed.
Example 2:
Input: nums = [1,1,1,1] Output: 6 Explanation: Each pair in the array are good.
Example 3:
Input: nums = [1,2,3] Output: 0
Constraints:
1 <= nums.length <= 1001 <= nums[i] <= 100
Video Tutorial
You can find the detailed video tutorial hereThought Process
Array is the most basic data structures and common solutions inclue
- Nested for loops O(N^2)
- Sort O(NlgN)
- Use extra space O(N)
This applies to this problem perfectly. The O(N^2) brute force solution is naive. We can also use a Map data structure (key is the number, value is the occurrence count) thus O(N). We can also sort the array and use this simple formula (also leetcode's hint) to calculate the good number pair.
Good pairs = N * (N-1) / 2 where N is how many duplicate numbers, this is from combination C(n^2), from n elements pick two
Solutions
Use Map
Space Complexity: O(N) since we use extra Map
Sort
Space Complexity: O(1) no extra space is used
References
- None
Saturday, July 4, 2020
System design interview: how to design a simple twitter search system
Methodology: READ MF!
[Originally from the Post: System design interview: how to design a chat system (e.g., Facebook Messenger, WeChat or WhatsApp)]Remind ourselves with the "READ MF!" methodology.
Requirements
Simple text based search with "AND" or "OR" support. E.g., give me all the tweets that have words "Black" AND "Life" in it sorted by published time in descending order.
search(api_dev_key, search_terms, maximum_results_to_return, sort, page_token)
A follow up question would be sort those results in other orders, E.g., give me all the tweets that have words "Black" AND "Life" in it sorted by the most commented tweets in descending order.
Estimation
- Storage: assuming twitter has 1B users, 50% of them post a tweet per day, each tweet is 140 char = 140 Byte. Each day, 1B * 0.5 * 280(roughly 300)Byte = 150GB data
- Write QPS = 1B user * 0.5 post a tweet per day / 86400 = 5787 QPS = 6000 QPS
- Query QPS = assuming 3x than write QPS = 18000 QPS
Write QPS in general we don't worry too much since it could be processed asynchronously. 18000 QPS for read is easy to handle as long as we have enough number of boxes and most of query would be returned via memory (not hitting disk).
Key designs and terms
A few key terminologies.
If the follow up question, we just need to build another index given the sort key or we could fetch the results on flight and sort (local optimal). Follow "Index -> Search -> Rank" steps.
Baozi Youtube Video
References (Credits to original authors)
Saturday, June 27, 2020
Leetcode solution 213. House Robber II
Problem Statement
You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed. All houses at this place are arranged in a circle. That means the first house is the neighbor of the last one. Meanwhile, adjacent houses have security system connected and it will automatically contact the police if two adjacent houses were broken into on the same night.
Given a list of non-negative integers representing the amount of money of each house, determine the maximum amount of money you can rob tonight without alerting the police.
Example 1:
Input: [2,3,2] Output: 3 Explanation: You cannot rob house 1 (money = 2) and then rob house 3 (money = 2), because they are adjacent houses.
Example 2:
Input: [1,2,3,1] Output: 4 Explanation: Rob house 1 (money = 1) and then rob house 3 (money = 3). Total amount you can rob = 1 + 3 = 4.Problem link
Video Tutorial
You can find the detailed video tutorial hereThought Process
This is very similar to House Robber I problem where the only difference is the houses now form a circle (French fancy way calls it cul-de-sac). It's same DP algorithm except now we need to consider two cases: whether we rob the first house or not. If we rob the first house, we should not rob the last house. If we do not rob the first house, we can rob the last house. We can even reuse the rob() function in House Robber I problem
Solutions
Use DP
Space Complexity: O(N) since we use extra arrays
References
Saturday, June 20, 2020
Leetcode solution 198. House Robber
Problem Statement
You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed, the only constraint stopping you from robbing each of them is that adjacent houses have security system connected and it will automatically contact the police if two adjacent houses were broken into on the same night.
Given a list of non-negative integers representing the amount of money of each house, determine the maximum amount of money you can rob tonight without alerting the police.
Example 1:
Input: nums = [1,2,3,1] Output: 4 Explanation: Rob house 1 (money = 1) and then rob house 3 (money = 3). Total amount you can rob = 1 + 3 = 4.
Example 2:
Input: nums = [2,7,9,3,1] Output: 12 Explanation: Rob house 1 (money = 2), rob house 3 (money = 9) and rob house 5 (money = 1). Total amount you can rob = 2 + 9 + 1 = 12.
Constraints:
0 <= nums.length <= 1000 <= nums[i] <= 400
Video Tutorial
You can find the detailed video tutorial hereThought Process
Easy problem and Dynamic Programming(DP) should jump into mind given it's only asking for max values (Just think about different combo we have to do without using DP, a little less than 2^N)
The mathematical induction formula is below, for any current max money at index i, you either choose to use the i-1 or i-2 + current house's money to not trigger police.
max[i] = max(max[i - 2] + a[i], max[i-1])Solutions
DP
Time Complexity: O(N) N is the array sizeSpace Complexity: O(N) since we used an extra array
References
Saturday, June 13, 2020
Leetcode solution 200. Number of Islands (Using BFS, DFS & Disjoint Set)
Problem Statement
Given a 2d grid map of '1's (land) and '0's (water), count the number of islands. An island is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.
Example 1:
Input: 11110 11010 11000 00000 Output: 1
Example 2:
Input: 11000 11000 00100 00011 Output: 3Problem link
Video Tutorial
You can find the detailed video tutorial hereThought Process
I have recorded a video back in 2015 (5 years ago, Geez time flies) using BFS and DFS. The essential idea is every time we see a land (i.e., "1"), we would trigger a BFS or DFS search to mark all the connected grids and increase the island counts to 1.
Another solution is to use Disjoint Set (aka Union Find). There is a generic solution where we could implement a DisjointSet data structure and perform "union" steps first to assign each grid a "parent". In the 2nd iteration we can perform "find" step to count how many distinct "parents", which is the number of islands.
A quick summary of some classic use cases
- Disjoint Set / Union Find (Disjoint set is the data structure while union find is the algorithm, people normally use it interchangeably) can often be used to solve if a graph is connected or not, such as phone contact problem (who knows who, how many isolated groups are there)
- To detect if a directed graph has cycle, use Kahn's algorithm for topological sort
- To detect if a un-directed graph has cycle
Solutions
Use BFS
Time Complexity: O(M*N), where M and N is row and col of grid matrix. Each grid is visited onceSpace Complexity: O(M*N) since we have to track the visited grids
Use DFS
Time Complexity: O(M*N), where M and N is row and col of grid matrix. Each grid is visited onceSpace Complexity: O(M*N) since we have to track the visited grids
Use Disjoint Set / Union Find
Time Complexity: O(M*N), where M and N is row and col of grid matrix. Each grid is visited onceSpace Complexity: O(M*N) since we have to track the visited grids using a map
References
Saturday, June 6, 2020
Leetcode solution 207. Course Schedule
Problem Statement
There are a total of numCourses courses you have to take, labeled from 0 to numCourses-1.
Some courses may have prerequisites, for example to take course 0 you have to first take course 1, which is expressed as a pair: [0,1]
Given the total number of courses and a list of prerequisite pairs, is it possible for you to finish all courses?
Example 1:
Input: numCourses = 2, prerequisites = [[1,0]] Output: true Explanation: There are a total of 2 courses to take. To take course 1 you should have finished course 0. So it is possible.
Example 2:
Input: numCourses = 2, prerequisites = [[1,0],[0,1]] Output: false Explanation: There are a total of 2 courses to take. To take course 1 you should have finished course 0, and to take course 0 you should also have finished course 1. So it is impossible.
Constraints:
- The input prerequisites is a graph represented by a list of edges, not adjacency matrices. Read more about how a graph is represented.
- You may assume that there are no duplicate edges in the input prerequisites.
1 <= numCourses <= 10^5
Video Tutorial
You can find the detailed video tutorial hereThought Process
It is a classic dependency graph problem. We can translate this problem to direct if there is a cycle in a directed graph or not. A text book solution is Kahn's algorithm for topological sorting. We can have a simple way to represent the graph or use a more proper adjacency lists (a little bit overkill for this problem though)Solutions
Use adjacency lists BFS
Time Complexity: O(V), since each vertex is visited only once during BFSSpace Complexity: O(V+E) since we use adjacency lists to represent a directed graph
Use simple hashmap BFS
Time Complexity: O(V), since each vertex is visited only once during BFS
Space Complexity: O(V) since we are using a hashmap
Use recursion DFS
Time Complexity: O(V), since each vertex is visited only once during BFS
Space Complexity: O(V) since we used a lookup hashmap for memorization purpose (not considering function stack space)
References
Saturday, May 30, 2020
Google Code Jam 2020 Qualification Round: Parenting Partnering Returns Solution
Problem Statement
Problem
Cameron and Jamie's kid is almost 3 years old! However, even though the child is more independent now, scheduling kid activities and domestic necessities is still a challenge for the couple.
Cameron and Jamie have a list of N activities to take care of during the day. Each activity happens during a specified interval during the day. They need to assign each activity to one of them, so that neither of them is responsible for two activities that overlap. An activity that ends at time t is not considered to overlap with another activity that starts at time t.
For example, suppose that Jamie and Cameron need to cover 3 activities: one running from 18:00 to 20:00, another from 19:00 to 21:00 and another from 22:00 to 23:00. One possibility would be for Jamie to cover the activity running from 19:00 to 21:00, with Cameron covering the other two. Another valid schedule would be for Cameron to cover the activity from 18:00 to 20:00 and Jamie to cover the other two. Notice that the first two activities overlap in the time between 19:00 and 20:00, so it is impossible to assign both of those activities to the same partner.
Given the starting and ending times of each activity, find any schedule that does not require the same person to cover overlapping activities, or say that it is impossible.
Input
The first line of the input gives the number of test cases, T. T test cases follow. Each test case starts with a line containing a single integer N, the number of activities to assign. Then, N more lines follow. The i-th of these lines (counting starting from 1) contains two integers Si and Ei. The i-th activity starts exactly Si minutes after midnight and ends exactly Ei minutes after midnight.
Output
For each test case, output one line containing Case #x: y, where x is the test case number (starting from 1) and y is IMPOSSIBLE if there is no valid schedule according to the above rules, or a string of exactly N characters otherwise. The i-th character in y must be C if the i-th activity is assigned to Cameron in your proposed schedule, and J if it is assigned to Jamie.
If there are multiple solutions, you may output any one of them. (See "What if a test case has multiple correct solutions?" in the Competing section of the FAQ. This information about multiple solutions will not be explicitly stated in the remainder of the 2020 contest.)
Limits
Time limit: 20 seconds per test set.
Memory limit: 1GB.
1 ≤ T ≤ 100.
0 ≤ Si < Ei ≤ 24 × 60.
Test set 1 (Visible Verdict)
2 ≤ N ≤ 10.
Test set 2 (Visible Verdict)
2 ≤ N ≤ 1000.
Sample
Input | Output |
4 3 360 480 420 540 600 660 3 0 1440 1 3 2 4 5 99 150 1 100 100 301 2 5 150 250 2 0 720 720 1440 | Case #1: CJC Case #2: IMPOSSIBLE Case #3: JCCJJ Case #4: CC |
Sample Case #1 is the one described in the problem statement. As mentioned above, there are other valid solutions, like JCJ and JCC.
In Sample Case #2, all three activities overlap with each other. Assigning them all would mean someone would end up with at least two overlapping activities, so there is no valid schedule.
In Sample Case #3, notice that Cameron ends an activity and starts another one at minute 100.
In Sample Case #4, any schedule would be valid. Specifically, it is OK for one partner to do all activities.
Problem link
Video Tutorial
You can find the detailed video tutorial hereThought Process
If you remember the leetcode "merge interval" question, this is quite similar. Baozi Training "Merge Interval"
Model the time range in internal, sort the intervals in ascending order based on the start time, then schedule either "C" or "J" as long as they are available. Update the end time with the assigned task.
The only caveat is we have to remember the original task index for output purpose because we sort the interval using the start time.
An alternate solution is a "bipartite graph coloring" problem. In essence, model the interval into an interval graph. Each interval is a vertex in the graph, and if it overlaps with another interval, there would be an edge. Now the problem becomes starting with one node, if we could color the nodes in two colors without any conflicts. Note the graph doesn't need to be fully connected, a simple BFS with a visited hash map should do the trick. https://www.geeksforgeeks.org/bipartite-graph/
The time complexity of "bipartite graph coloring" is O(V+E)
Solutions
Greedy solution
Time Complexity: O(lgN) since we sortSpace Complexity: O(N) since we used extra list for the intervals
References
Saturday, May 23, 2020
Google Code Jam 2020 Qualification Round: Nesting Depth Solution
Problem Statement
Problem
tl;dr: Given a string of digits S, insert a minimum number of opening and closing parentheses into it such that the resulting string is balanced and each digit d is inside exactly d pairs of matching parentheses.
Let the nesting of two parentheses within a string be the substring that occurs strictly between them. An opening parenthesis and a closing parenthesis that is further to its right are said to match if their nesting is empty, or if every parenthesis in their nesting matches with another parenthesis in their nesting. The nesting depth of a position p is the number of pairs of matching parentheses m such that p is included in the nesting of m.
For example, in the following strings, all digits match their nesting depth: 0((2)1), (((3))1(2)), ((((4)))), ((2))((2))(1). The first three strings have minimum length among those that have the same digits in the same order, but the last one does not since ((22)1) also has the digits 221 and is shorter.
Given a string of digits S, find another string S', comprised of parentheses and digits, such that:
- all parentheses in S' match some other parenthesis,
- removing any and all parentheses from S' results in S,
- each digit in S' is equal to its nesting depth, and
- S' is of minimum length.
Input
The first line of the input gives the number of test cases, T. T lines follow. Each line represents a test case and contains only the string S.
Output
For each test case, output one line containing Case #x: y, where x is the test case number (starting from 1) and y is the string S' defined above.
Limits
Time limit: 20 seconds per test set.
Memory limit: 1GB.
1 ≤ T ≤ 100.
1 ≤ length of S ≤ 100.
Test set 1 (Visible Verdict)
Each character in S is either 0 or 1.
Test set 2 (Visible Verdict)
Each character in S is a decimal digit between 0 and 9, inclusive.
Sample
Input | Output |
4 0000 101 111000 1 | Case #1: 0000 Case #2: (1)0(1) Case #3: (111)000 Case #4: (1) |
The strings ()0000(), (1)0(((()))1) and (1)(11)000 are not valid solutions to Sample Cases #1, #2 and #3, respectively, only because they are not of minimum length. In addition, 1)( and )(1 are not valid solutions to Sample Case #4 because they contain unmatched parentheses and the nesting depth is 0 at the position where there is a 1.
You can create sample inputs that are valid only for Test Set 2 by removing the parentheses from the example strings mentioned in the problem statement.
Problem link
Video Tutorial
You can find the detailed video tutorial hereThought Process
Simple simulation. Key points
- An integer could be used for depth to record how many parentheses we need to append. (I used a stack in the code during the competition)
- We could use a dummy node as the depth is 0 instead of starting from index 1.
Solutions
Simulation solution
Time Complexity: O(N)Space Complexity: O(N) since we used extra extra space to store the output
References
Subscribe to:
Posts (Atom)