Problem Statement
There is a street with n * 2 plots, where there are n plots on each side of the street. The plots on each side are numbered from 1 to n. On each plot, a house can be placed.
Return the number of ways houses can be placed such that no two houses are adjacent to each other on the same side of the street. Since the answer may be very large, return it modulo 109 + 7.
Note that if a house is placed on the ith plot on one side of the street, a house can also be placed on the ith plot on the other side of the street.
Example 1:
Input: n = 1 Output: 4 Explanation: Possible arrangements: 1. All plots are empty. 2. A house is placed on one side of the street. 3. A house is placed on the other side of the street. 4. Two houses are placed, one on each side of the street.
Example 2:
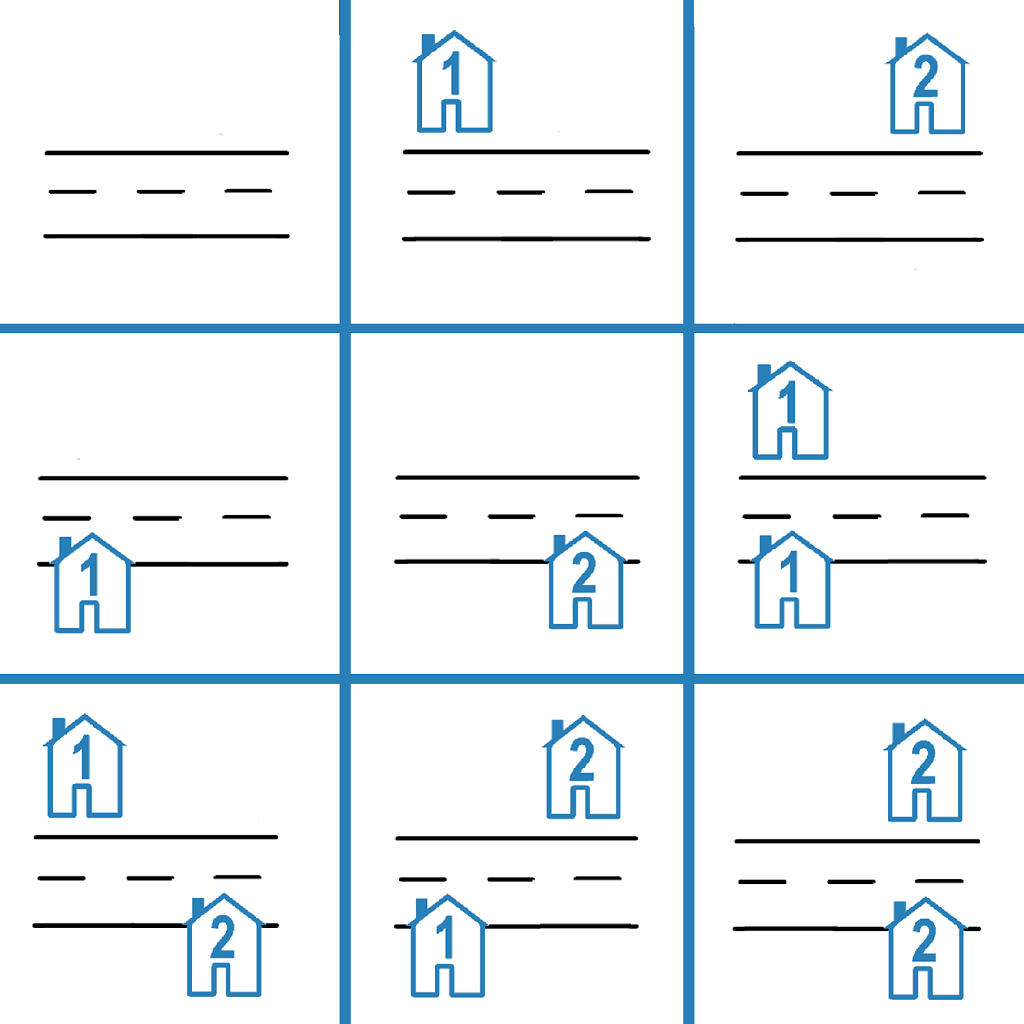
Input: n = 2 Output: 9 Explanation: The 9 possible arrangements are shown in the diagram above.
Constraints:
1 <= n <= 104
Video Tutorial
You can find the detailed video tutorial hereThought Process
A classic DP problem (Dynamic Programming)
because it's either ask you a boolean yes or no questions, Or ask for
extreme values, e.g., min, max, or just a number of solutions etc.
- Two sides are independent, each side is similar to Climb Stairs, House Robber House Robber II
- Given each side is independent, the combo would be multiplied together.
- Implementation wise
- could use two variables to replace the array
- be careful about overflow (use long to cast back to int)
Solutions
Space Complexity: O(1) if we use two variables to track, the above implementation is O(N) since an extra array is used.