Leetcode solution 1292: Maximum Side Length of a Square with Sum Less than or Equal to Threshold

Problem Statement 

Given a m x n matrix mat and an integer threshold. Return the maximum side-length of a square with a sum less than or equal to threshold or return 0 if there is no such square.

Example 1:

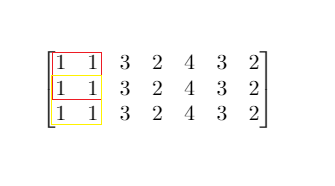
Input: mat = [[1,1,3,2,4,3,2],[1,1,3,2,4,3,2],[1,1,3,2,4,3,2]], threshold = 4
Output: 2
Explanation: The maximum side length of square with sum less than 4 is 2 as shown.

Example 2:

Input: mat = [[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2]], threshold = 1
Output: 0

Example 3:

Input: mat = [[1,1,1,1],[1,0,0,0],[1,0,0,0],[1,0,0,0]], threshold = 6
Output: 3

Example 4:

Input: mat = [[18,70],[61,1],[25,85],[14,40],[11,96],[97,96],[63,45]], threshold = 40184
Output: 2

Constraints:

• 1 <= m, n <= 300
• m == mat.length
• n == mat[i].length
• 0 <= mat[i][j] <= 10000
• 0 <= threshold <= 10^5

 Problem link

Video Tutorial

You can find the detailed video tutorial here

• Youtube
• B站

Thought Process

There is an absolute brute force way is to calculate the sum of each square in every iteration. There are previous similar problems that we can have a prefix sum matrix, similar to the rolling sum idea on one dimensional array.

A prefix sum matrix is a matrix that for each cell[i, j] represents the sum in original matrix from matrix[0, 0] to matrix [i, j] (inclusive)

The advantage is later we can get any rectangle sum simply performing below

sum from [i, j] to [i + len][j + len] = prefixSum[i + len][j + len] - prefixSum[i - 1][j + len] - prefixSum[i + len][j - 1] + prefixSum[i - 1][j - 1]

Two more optimizations we can do

• We can apply binary search instead of a linear one to find the max length
• We can also keep a record of the sum while building up the prefix sum matrix. The reason this works is if it has a square say 3x3 that meets the requirement, then it would definitely have a square 2x2 meet the requirement. So we can start from 1x1, 2x2 till we reach the max. Pretty smart! Kudos to @drunkpiano

• Reference is here: Leetcode discussion solution with binary search and smart solution

Solutions

Prefix sum implementation

Time Complexity: O(M*N*min(M,N)) where M is row N is col, essentially O(N^3)
Space Complexity: O(M*N) since we need

References

• Leetcode discussion solution with binary search and smart solution
• Leetcode discussion normal

Leetcode solution 229: Major Element II

Problem Statement 

Given an integer array of size n, find all elements that appear more than ⌊ n/3 ⌋ times.

Note: The algorithm should run in linear time and in O(1) space.

Example 1:

Input: [3,2,3]
Output: [3]

Example 2:

Input: [1,1,1,3,3,2,2,2]
Output: [1,2]

 Problem link

Video Tutorial

You can find the detailed video tutorial here

• Youtube
• B站

Thought Process

It's a follow up question on Majority Element, given the hint, there should only be at most 2 elements that can satisfy the requirement (You cannot have 3 elements that all appear more than n/3 times). We can perform the voting algorithm on two potential candidates and later do an actual sum to eliminate the false positive (e.g., [1, 2, 1] would have both 1 and 2 as potential candidate, but 2 should not be included)

You can refer to Majority Element for a detailed explanation on the voting algorithm.

An extension could be changing n/3 to n/k. We just need extra arrays to store votes and candidates. It will take O(Nk) time complexity

Solutions

Voting implementation

Time Complexity: O(N) where N is the array size
Space Complexity: O(1) Constant space

References

• Leetcode discussion solution

Leetcode solution 169: Major Element

Problem Statement 

Given an array of size n, find the majority element. The majority element is the element that appears more than ⌊ n/2 ⌋ times.

You may assume that the array is non-empty and the majority element always exist in the array.

Example 1:

Input: [3,2,3]
Output: 3

Example 2:

Input: [2,2,1,1,1,2,2]
Output: 2

 Problem link

Video Tutorial

You can find the detailed video tutorial here

• Youtube
• B站

Thought Process

Simple but great question that can be solved in many ways, the voting one approves to be the most time and space efficient solution.

You can refer to Leetcode official solution for a detailed explanation.

Solutions

Voting implementation

Time Complexity: O(N) where N is the array size
Space Complexity: O(1) Constant space

References

• Leetcode official solution

Leetcode solution 6: ZigZag Conversion

Problem Statement 

The string "PAYPALISHIRING" is written in a zigzag pattern on a given number of rows like this: (you may want to display this pattern in a fixed font for better legibility)

P   A   H   N
A P L S I I G
Y   I   R

And then read line by line: "PAHNAPLSIIGYIR"

Write the code that will take a string and make this conversion given a number of rows:

string convert(string s, int numRows);

Example 1:

Input: s = "PAYPALISHIRING", numRows = 3
Output: "PAHNAPLSIIGYIR"

Example 2:

Input: s = "PAYPALISHIRING", numRows = 4
Output: "PINALSIGYAHRPI"
Explanation:

P     I    N
A   L S  I G
Y A   H R
P     I

 Problem link

Video Tutorial

You can find the detailed video tutorial here

• Youtube
• B站

Thought Process

It's a very good implementation problem, by simply simulating each character in the string to each row, it would take extra O(N) space to hold up the array where N is the string size. However, there is definitely a difference between a good and poor implementation.

There is also a math formula we can use, please see attached pdf for solutions.

Solutions

Simulation poor implementation

Time Complexity: O(N) where N is the string size
Space Complexity: O(N) since we used an extra array to store each character in the string

Simulation good implementation

Time Complexity: O(N) where N is the string size
Space Complexity: O(N) since we used an extra array to store each character in the string

References

• Leetcode official solution