Leetcode solution 59: Sprial Matrix II

Problem Statement 

Given a positive integer n, generate a square matrix filled with elements from 1 to n² in spiral order.

Example:

Input: 3
Output:
[
 [ 1, 2, 3 ],
 [ 8, 9, 4 ],
 [ 7, 6, 5 ]
]

 Problem link

Video Tutorial

You can find the detailed video tutorial here

• Youtube
• B站

Thought Process

Straight forward question, could use Spiral Matrix exact same recursion algorithm to solve this, you can also watch that video tutorial here

Still needs pay attribute to this guy, had another great solution:
https://leetcode.com/problems/spiral-matrix-ii/discuss/22282/4-9-lines-Python-solutions

Solutions

Simulation using Recursion

Time Complexity: O(M*N) where M, N is row and col of matrix
Space Complexity: O(M*N) since we used list to store the result, where M, N is row and col of matrix

References

• Spiral Matrix

System design interview: how to design a feeds system (e.g., Twitter, Instagram and Facebook news feed)

System design interview: how to design a feeds system (e.g., Twitter, Instagram and Facebook news feed)

Methodology: READ MF!

Please use this "READ MF!" framework for software engineer system interview purpose.

Key designs and terms 

• So far the best detailed explanation on designing twitter is from Raffi (used to be VP of Twitter) on QCon. Presentation, Slides [All credits go to QCon). Raffi is very smart and articulate, really solid guy!
• Read heavy system, not write heavy, optimized for user timeline. To be clear, there are two timelines, one is user's own tweets (easy to do), the other is the main timeline which is an aggregation of all the tweets from the people that user follows. 
• Pre-calculate all the timelines. This is the interesting part of the design vs using a mysql and having index to query in realtime, which would not be scalable. When a tweet is posted, the tweets service would
• Store this tweet in memory, and that later would be flushed to a main DB
• Call the fanout deliver service to publish this tweet to all the users' timeline that followed this particular user. It could simply store a tweet ID (and later the content could be retrieved from the Tweets Cache) or hydrating the entire text content is also fine (note how we want to handle eidt or delete, twitter probably doesn't allow delete)
• Call search service to index (Lucene). The search index is also hosted in memory on Redis. Note search here needs to fanout to all search clusters but due to the in memory hosting, it's acceptable.
• Always remember disk access is at least 100k times slower than memory access, e.g, disk is 10ms vs 100ns on memory. https://gist.github.com/jboner/2841832
• With the pre-caculate timeline design, there might be race conditions when celebrity (people with millions of followers) starts to talking to each other with replies. E.g., celebrity A tweets something, takes 30 sec to deliver to all the followers,  celebrity B replies before deliver finishes, some followers follow both A and B might see B's reply first before A's original post. One cheat workaround is to sort by timestamp or tweet IDs, but they are also experimenting with only pre-calculate non-celebrity tweets, and when generating timeline, realtime fetching the celebrity tweets. It depends which way is better and also the user experience. This is a good stop point to talk to your interviewers in real world about tradeoffs.
• Since twitter is heavily relying on cache, you might want to checkout how they optimized the caching with twemproxy.

Baozi Youtube Video

• Youtube Raffi Video, Slides 
• Youtube Baozi Video
• B站

Leetcode solution 54: Sprial Matrix

Problem Statement 

Given a matrix of m x n elements (m rows, n columns), return all elements of the matrix in spiral order.

Example 1:

Input:
[
 [ 1, 2, 3 ],
 [ 4, 5, 6 ],
 [ 7, 8, 9 ]
]
Output: [1,2,3,6,9,8,7,4,5]

Example 2:

Input:
[
  [1, 2, 3, 4],
  [5, 6, 7, 8],
  [9,10,11,12]
]
Output: [1,2,3,4,8,12,11,10,9,5,6,7]

 Problem link

Video Tutorial

You can find the detailed video tutorial here

• Youtube
• B站

Thought Process

It's a straight forward implementation question, we can simply just simulate the spiral order and print. You can choose to do it either iteratively (see reference to download the official Leetcode solution) or use recursion.

There is this awesome one line solution from this guy which is pretty insane.

def spiralOrder(self, matrix):
    return matrix and list(matrix.pop(0)) + self.spiralOrder(zip(*matrix)[::-1])

https://leetcode.com/problems/spiral-matrix/discuss/20571/1-liner-in-Python-%2B-Ruby

Solutions

Simulation using Recursion

Time Complexity: O(M*N) where M, N is row and col of matrix
Space Complexity: O(M*N) since we used list to store the result, where M, N is row and col of matrix

References

• Leetcode official solution (download pdf)

Leetcode solution 322: Coin Change

Problem Statement 

You are given coins of different denominations and a total amount of money amount. Write a function to compute the fewest number of coins that you need to make up that amount. If that amount of money cannot be made up by any combination of the coins, return -1. Example 1:

Input: coins = [1, 2, 5], amount = 11
Output: 3 
Explanation: 11 = 5 + 5 + 1

Example 2:

Input: coins = [2], amount = 3
Output: -1

Problem link

Video Tutorial

You can find the detailed video tutorial here

• Youtube
• B站

Thought Process

This is a classic problem and greedy might be the first thing comes into mind. For example, sort the coins on denomination and always use the largest amount coin. However, the optimal solution might not include the largest denomination.

for example , [1, 3, 4] and target value 6. The optimal is two 3s, not [4, 1, 1].

It seems we have to list out all the different combinations and find the min value, that leads to a brute fore solution as described here using recursion. It would be an exponential time complexity.

We can use a hash map as a lookup to remember for each amount, what would be the min cost. That would significantly reduce the time complexity from exponential to O(S*N) where S is the amount and N is the coins array size. It's not obvious why but once you see the DP solution, you can understand better, it's the same time complexity.

Another way is to use dynamic programming because the problem is asking for a single yes/no, extreme value(min, max), building up a lookup table using formula is the coding pattern. We have similar problems, Wild Card Matching, Regular Expression Matching

The idea is to build a lookup table for each amount, what's the minimal number of coins needed given current  denomination.

lookup[i] = min(lookup[i], lookup[i - coin value] + 1) given i - coin value >= 0

Solutions

Dynamic Programming

Time Complexity: O(S*N) where S is the amount and N is the coins array size
Space Complexity: O(N) since we used a lookup array

References

• Leetcode official solution (download pdf)

Leetcode solution 274: H-Index

包子小道消息@12/07/2019

从growth at all cost 到profitability mindset，都是被Uber Wework ​弄得。软银老板Masa的头发估计又得脱落几根，不过airbnb也许是2020年被大家追捧的一个新星，从cash at hand / total funds raised 的比例来看，就是下一个google，Facebook和zoom的节奏啊！

 

Problem Statement 

Given an array of citations (each citation is a non-negative integer) of a researcher, write a function to compute the researcher's h-index.

According to the definition of h-index on Wikipedia: "A scientist has index h if h of his/her N papers have at least h citations each, and the other N − h papers have no more than h citations each."

Example:

Input: citations = [3,0,6,1,5]
Output: 3 
Explanation: [3,0,6,1,5] means the researcher has 5 papers in total and each of them had 
             received 3, 0, 6, 1, 5 citations respectively. 
             Since the researcher has 3 papers with at least 3 citations each and the remaining 
             two with no more than 3 citations each, her h-index is 3.

Note: If there are several possible values for h, the maximum one is taken as the h-index.

Hint 1
An easy approach is to sort the array first.
Hint 2
What are the possible values of h-index?
Hint 3
A faster approach is to use extra space. 

Problem link

Video Tutorial

You can find the detailed video tutorial here

• Youtube
• B站

Thought Process

It’s not the most straightforward question to understand I have to admit that. I normally start with small examples to help me understand

The requirement is: his/her N papers have at least h citations each, and the other N − h papers have no more than h citations each

What happens if citation contains only 1 element?

• Citations = [100] , N = 1, h = 1, N-h = 0

This gives us hint that h has an upper bound of N

What happens if citation contains only 2 elements? And we can assign some large citation values

• Citations = [1000, 2000] , N = 2, h = 2. It seems h-index has not too much to do with the citation values itself, rather it’s about the index and the values.

We should now have a super brute force way, since h is bounded to be [0, N], we just go through each value and try to see if it could meet the h criteria (e.g., we start from N, then we see if there is at least N papers that have at least N citations) This would result in a O(N^2) time complexity.

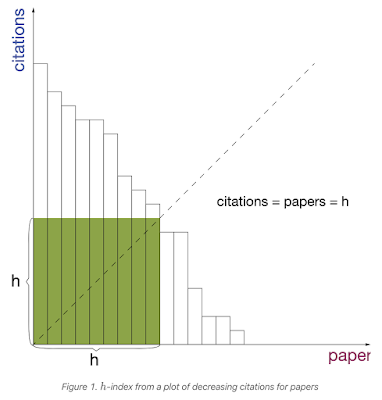
Naturally, we normally can think of if we can sort the array to reduce the time complexity. After sort, using the below graph, the problem becomes find the citation more than the citation array index, and that citation index could be the h-index (that's why it's called h-index, not h-value, it's about index). This would give a O(NlgN) time complexity. Code is attached in the References section. 

source: leetcode solution

Finally, we can think about bucket sort since h-index is bounded from [0, N], and if paper citations are larger than N, it's just considered on counting on index N.

You know how to do a bucket sort 😄

Solutions

Use bucket sort

Time Complexity: O(N) since we went through citations only once
Space Complexity: O(N) since we are using an extra array to keep track of the count

References

• Leetcode official solution (download pdf)