Leetcode solution 173: Binary Search Tree Iterator

Problem Statement 

Implement an iterator over a binary search tree (BST). Your iterator will be initialized with the root node of a BST.

Calling next() will return the next smallest number in the BST.

Example:

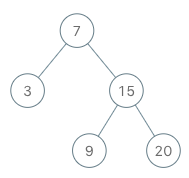
BSTIterator iterator = new BSTIterator(root);
iterator.next();    // return 3
iterator.next();    // return 7
iterator.hasNext(); // return true
iterator.next();    // return 9
iterator.hasNext(); // return true
iterator.next();    // return 15
iterator.hasNext(); // return true
iterator.next();    // return 20
iterator.hasNext(); // return false

Note:

• next() and hasNext() should run in average O(1) time and uses O(h) memory, where h is the height of the tree.
• You may assume that next() call will always be valid, that is, there will be at least a next smallest number in the BST when next() is called.

Problem link

 

Video Tutorial

You can find the detailed video tutorial here

• Youtube
• B站

Thought Process

 

Brute force dump tree into array method

It’s very similar to BST in order traversal. From that train of thought , we can easily have a brute force solution: perform an in-order traversal, dump that order into an array. Then we can have an pointer point to the array and move the pointer forward every time we call next() method. The time complexity of this brute force way is O(N) in the constructor phase (N is the total number of nodes in the tree). Even though we iterate through the tree 2 times, it’s still O(N), hasNext() and Next() would all be O(1). Space complexity is O(N) as well since we need an extra array to store all the elements in the tree.

Brute force way to dump the tree into an array then iterate over the array
Image credit: https://leetcode.com/articles/binary-search-tree-iterator/

In order traversal using stack  

 

In order to reduce memory from O(N) to O(lgN), aka O(h) where h is the height of the tree, an alternative is return the next() inline while we are performing the recursion. The tricky part is if we still perform the in-order traversal using recursion, there is no easier way to plug in the next() method into the recursion call.

We know we can always use stack to simulate recursion (the push function stack part), and by having a tree node in the stack, it’s also easier to track the predecessor  and successor. The starting position should point to the smallest node in the tree, which is the left most node, we keep going left and pushing the nodes we visited to the stack. Whenever next() is called, we return the top of the stack, and we check if there is any right child of the node, if so, continue push the nodes into the stack until we hit the left most one. hasNext() is simply checking if there is still nodes in the stack. The time complexity of next() would be average O(1) even we have a while loop to keep finding the left most child since on high level, each node is still visited only once. Space complexity is O(lgN) since we at most would put the height of tree worth of elements into the stack.

Initial stage
Image credit: https://leetcode.com/articles/binary-search-tree-iterator/

Find the left most child
Image credit: https://leetcode.com/articles/binary-search-tree-iterator/

Solutions

In order traversal using stack

Note in next() method, we don't need to check if there is still element left in the stack. It is the caller's responsibility to check so. It is described in the Java's Iterator interface NoSuchElementException should be thrown.



Time Complexity: next(), hasNext() O(1) on average even with the while loop, think each node is visited essentially only once
Space Complexity: O(lgN), extra stack is needed capped at tree height

References

• Leetcode official solution