Problem Statement
You are given a 0-indexed m x n integer matrix grid consisting of distinct integers from 0 to m * n - 1. You can move in this matrix from a cell to any other cell in the next row. That is, if you are in cell (x, y) such that x < m - 1, you can move to any of the cells (x + 1, 0), (x + 1, 1), ..., (x + 1, n - 1). Note that it is not possible to move from cells in the last row.
Each possible move has a cost given by a 0-indexed 2D array moveCost of size (m * n) x n, where moveCost[i][j] is the cost of moving from a cell with value i to a cell in column j of the next row. The cost of moving from cells in the last row of grid can be ignored.
The cost of a path in grid is the sum of all values of cells visited plus the sum of costs of all the moves made. Return the minimum cost of a path that starts from any cell in the first row and ends at any cell in the last row.
Example 1:
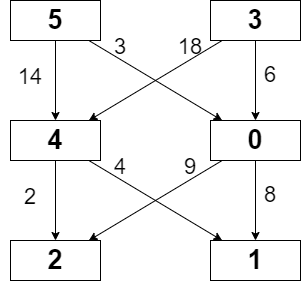
Input: grid = [[5,3],[4,0],[2,1]], moveCost = [[9,8],[1,5],[10,12],[18,6],[2,4],[14,3]] Output: 17 Explanation: The path with the minimum possible cost is the path 5 -> 0 -> 1. - The sum of the values of cells visited is 5 + 0 + 1 = 6. - The cost of moving from 5 to 0 is 3. - The cost of moving from 0 to 1 is 8. So the total cost of the path is 6 + 3 + 8 = 17.
Example 2:
Input: grid = [[5,1,2],[4,0,3]], moveCost = [[12,10,15],[20,23,8],[21,7,1],[8,1,13],[9,10,25],[5,3,2]] Output: 6 Explanation: The path with the minimum possible cost is the path 2 -> 3. - The sum of the values of cells visited is 2 + 3 = 5. - The cost of moving from 2 to 3 is 1. So the total cost of this path is 5 + 1 = 6.
Constraints:
m == grid.lengthn == grid[i].length2 <= m, n <= 50gridconsists of distinct integers from0tom * n - 1.moveCost.length == m * nmoveCost[i].length == n1 <= moveCost[i][j] <= 100
Video Tutorial
You can find the detailed video tutorial hereThought Process
- Build up a minCost 2 day array, each array element denotes by far the min cost to reach to that element
- Make sure to initialize the values.

Solutions
References
- None

No comments:
Post a Comment
Thank your for your comment! Check out us at https://baozitraining.org/ if you need mock interviews!