Leetcode solution 1292: Maximum Side Length of a Square with Sum Less than or Equal to Threshold

Problem Statement 

Given a m x n matrix mat and an integer threshold. Return the maximum side-length of a square with a sum less than or equal to threshold or return 0 if there is no such square.

Example 1:

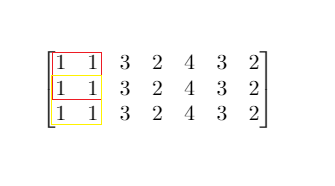
Input: mat = [[1,1,3,2,4,3,2],[1,1,3,2,4,3,2],[1,1,3,2,4,3,2]], threshold = 4
Output: 2
Explanation: The maximum side length of square with sum less than 4 is 2 as shown.

Example 2:

Input: mat = [[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2]], threshold = 1
Output: 0

Example 3:

Input: mat = [[1,1,1,1],[1,0,0,0],[1,0,0,0],[1,0,0,0]], threshold = 6
Output: 3

Example 4:

Input: mat = [[18,70],[61,1],[25,85],[14,40],[11,96],[97,96],[63,45]], threshold = 40184
Output: 2

Constraints:

• 1 <= m, n <= 300
• m == mat.length
• n == mat[i].length
• 0 <= mat[i][j] <= 10000
• 0 <= threshold <= 10^5

 Problem link

Video Tutorial

You can find the detailed video tutorial here

• Youtube
• B站

Thought Process

There is an absolute brute force way is to calculate the sum of each square in every iteration. There are previous similar problems that we can have a prefix sum matrix, similar to the rolling sum idea on one dimensional array.

A prefix sum matrix is a matrix that for each cell[i, j] represents the sum in original matrix from matrix[0, 0] to matrix [i, j] (inclusive)

The advantage is later we can get any rectangle sum simply performing below

sum from [i, j] to [i + len][j + len] = prefixSum[i + len][j + len] - prefixSum[i - 1][j + len] - prefixSum[i + len][j - 1] + prefixSum[i - 1][j - 1]

Two more optimizations we can do

• We can apply binary search instead of a linear one to find the max length
• We can also keep a record of the sum while building up the prefix sum matrix. The reason this works is if it has a square say 3x3 that meets the requirement, then it would definitely have a square 2x2 meet the requirement. So we can start from 1x1, 2x2 till we reach the max. Pretty smart! Kudos to @drunkpiano

• Reference is here: Leetcode discussion solution with binary search and smart solution

Solutions

Prefix sum implementation

Time Complexity: O(M*N*min(M,N)) where M is row N is col, essentially O(N^3)
Space Complexity: O(M*N) since we need

References

• Leetcode discussion solution with binary search and smart solution
• Leetcode discussion normal